
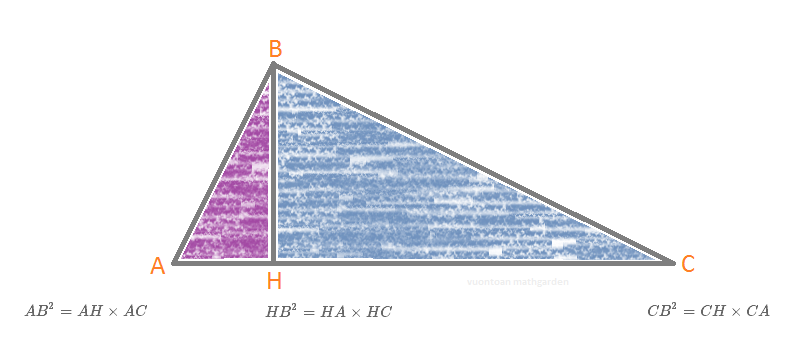
angle bisectors, altitudes and medians of t triangles. The measure of the altitude drawn from the vertex of the right angle to the hypotenuse is the geometric mean between the measures of the two segments of the hypotenuse. u00a9 2012 Holt McDougal, Larson Resources. The altitude A E is perpendicular to side B C. The vertices are at the points (0,0), (0,8), and (6,0). This is the required equation of the altitude from C to A B. $$\triangle ABC\sim \triangle BCD\sim\triangle ABD$$ Directions: The black triangle is a right triangle with legs 8 and 6. Each leg is the geometric mean of the hypotenuse and the segment of. Items may require the use of the geometric mean. 12 Altitude in a Right Triangle In a right triangle, the altitude from the right angle to the hypotenuse divides the hypotenuse into two segments. The altitude is the geometric mean of the segments into which it separates the hypotenuse. The two triangles formed are also similar to each other. relationships involving an altitude drawn to the hypotenuse of a right triangle.
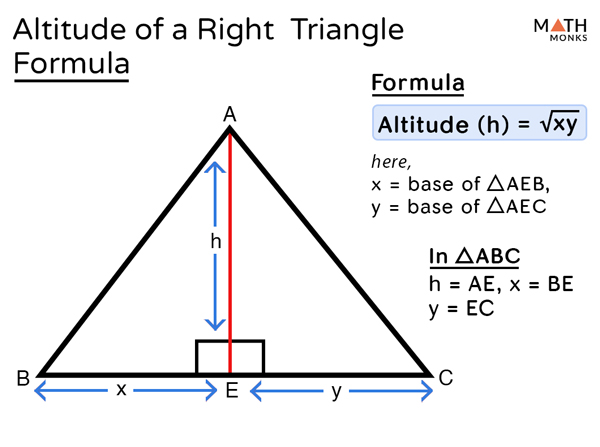
If we in the following triangle draw the altitude from the vertex of the right angle then the two triangles that are formed are similar to the triangle we had from the beginning. The proportion 2:x=x:4 must be true hence

Thank you.The geometric mean is the positive square root of the product of two numbers. C So the sites will be proportional so we can write Ah, you can write as a by B or B by a be by a equal toe be by a quilter, see by B So when clock we cross multiply, it becomes be be equal toe a C which we needed toe prove So this is that proof. That is common so we can see that triangle ABC is similar to triangle B D. And we have this angle as common in both the both of these triangles so we can write and girl bc mm congress to angle B C D. The altitude of a triangle refers to the line segment that can join the vertex of a triangle and the opposite side of the triangle in a way so that the line. All are both have right angles that in 90 degrees. If we look at the triangles, triangles, ABC and jangles uh, a b c N c d b are tangle b d c. In right ABC shown above, altitude CD is drawn to the hypotenuse, forming two smaller right triangles they are. Right Triangle Altitude Theorem: This theorem describes the relationship between altitude drawn on the hypotenuse from vertex of the right angle and the. Sorry, this is C and happiness has be so We have to prove that to prove be in Toby equal toe and to see that we need to prove okay, we'll be using the similarity off triangles. Using a Geometric Mean To Solve Problems. Let us is you this as a decide, as be in happiness. Altitudes can be used in the computation of the area of a triangle. It is a special case of orthogonal projection. The process of drawing the altitude from the vertex to the foot is known as dropping the altitude at that vertex. Let us assume this to be p and product off length off this perpendicular B and a c length of a city that is happening in this will be called to length of baby into BC. The length of the altitude, often simply called 'the altitude', is the distance between the extended base and the vertex. One is 3, 4, 5, which we can scale up to 12, 16, 20 (note the hypotenuse of 20 in your figure). If ABC is right angle triangle, then if you drop perpendicular from B to the side A C let us assume b d then length of this beady that is. The simplest way, which will not work all the time, is that any time you see right triangles you should think about Pythagorean triples. We have to build that that in right angle Triangle? Yeah, we have a right angle triangle being given if we draw perpendicular from the right angle, that is from here. We have 1000 before they to on the pitch.


 0 kommentar(er)
0 kommentar(er)
